数据库专题训练

Similarity search

任务

实现近似串查询，近似串有两种度量方式：Levenshtein edit distance和Jaccard index。需要实现SimSeacher类的createIndex、searchED、searchJaccard三个方法。

代码中实现了brute-force、tournament sort、MergeSkip@LLL08和DivideSkip@LLL08四种查询算法。

BruteForce

枚举所有字符串，和查询字符串一一进行Levenshtein edit distance或Jaccard index的计算， 若满足阈值条件则添加到存放结果的向量。

Tournament sort

采用filter-and-verification framework，代码中实现了索引、Filter和Verification三个部分。

索引

索引的数据结构是若干倒排索引，另外有一个hash table为Q-gram到倒排索引的映射。

执行createIndex构建索引时， 对于每个输入的字串，使用类似Rabin-Karp string search算法的方式，获取当前长为的窗口中的Q-gram，计算出散列值，找到对应的倒排索引，并在该索引末端加入当前行号。如果输入字串有重复的Q-gram，那么当前行号可能会在倒排索引中插入多次。然后窗口向右移动一格，把之前的散列值通过rolling hash计算出下一时刻的值。

输入文件读入完毕后，对于hash table中的每个倒排索引(必然是非空的)，在末端加入作为哨兵元素的无穷大。

Filter

对于一个查询，使用类似构建索引时的Rabin-Karp string search algorithm，对于每个长为的窗口中的Q-gram，找到对应的倒排索引，把指向首元素的指针放入列表中。设查询字串长度位，那么中将会有个指针(可能重复)。

建立binary heap

列表的元素是指向倒排索引的指针，以指针指向的值为关键字使用Floyd’s algorithm 在时间内建立binary heap 。

Tournament sort进行N-way merge

1. 堆顶指针指向的值为，若old为无穷大则返回

2. 计算堆顶元素指向的值的出现次数，若大于等于阈值则添加到候选集中

3. 把堆顶元素指针向前移动一格(即指向对应的倒排索引的下一项)，若下一项仍等于原来指向的值则继续移动

4. 上述操作后堆顶指针指向的值变大了，对它进行下滤操作

5. 若新的堆顶指向的值等于则跳转到步骤3

之后对候选集的每个元素进行检验，是否满足Jaccard index或Levenshtein编辑距离的阈值要求， 输出筛选后的。

Verification

Levenshtein edit distance

对于searchED操作，需要对每个候选字串和查询字串计算编辑距离。

两个字符串的Levenshtein edit distance可以使用的Needleman–Wunsch algorithm计算。

注意到代码中使用到编辑距离的地方都有阈值限制，如果编辑距离超过阈值，那么它的实际值无关紧要。因此我们可以只计算动态规划矩阵中对角线带状区域的状态。

另外当其中某个字符串的长度小于等于128时，还可以采用bit vector的算法@edit03加速到。

Jaccard index

采用scan count的方式。 先用rolling hash计算查询串所有Q-gram的标号，在计数容器中增加一。然后对于候选串的所有Q-gram，若计数容器中的值大于零则减去零并加到答案中。再便利候选串的所有Q-gram，把减去的值再加回来。

MergeSkip

和tournament sort基本结构相同，对Filter部分做了优化，即优化了统计每个字串的出现次数，过程如下：

1. 堆顶指针指向的值为，若old为无穷大则返回

2. 计算堆顶元素指向的值的出现次数，若大于等于阈值则添加到候选集中

3. 把堆顶元素指针向前移动一格(即指向对应的倒排索引的下一项)，若下一项仍等于原来指向的值则继续移动

4. 上述操作后堆顶指针指向的值变大了，对它进行下滤操作

5. 若新的堆顶指向的值等于则跳转到步骤3

6. 从堆中弹出个元素，使用二分检索把这些倒排索引指针移动至大于当前堆顶指向的值，再重新插入堆中

DivideSkip

结合了MergeSkip和MergeOut。

1. 使用启发函数把倒排索引划分为长索引和短索引两类，长索引有个，其中为索引个数

2. 对短索引采用MergeSkip算法，对于短索引中所有出现次数不少于的元素，在所有长索引中二分检索

3. 将出现次数不少于的元素添加到候选集中

4. 把堆顶元素指针向前移动一格(即指向对应的倒排索引的下一项)，若下一项仍等于原来指向的值则继续移动

5. 上述操作后堆顶指针指向的值变大了，对它进行下滤操作

6. 若新的堆顶指向的值等于则跳转到步骤4

7. 从堆中弹出个元素，使用二分检索把这些倒排索引指针移动至大于当前堆顶指向的值，再重新插入堆中

其他

Tournament类使用了curiously recurring template pattern。

Similarity join

任务

实现similarity join，近似串有两种度量方式：Levenshtein edit distance和Jaccard index。需要实现SimJoiner类的joinED、joinJaccard两个方法。

BruteForce

枚举集合的所有字符串，和集合的所有字符串一一进行Levenshtein edit distance或Jaccard index的计算，若满足阈值条件则添加到存放结果的向量，实现复杂度为，其中为串的最大长度。

DivideSkip

执行次similarity search。 采用filter-and-verification framework，代码中实现了索引、Filter和Verification三个部分。

索引

索引的数据结构是若干倒排索引，另外有一个hash table为Q-gram到倒排索引的映射。

执行createIndex构建索引时， 对于每个输入的字串，使用类似Rabin-Karp string search算法的方式，获取当前长为的窗口中的Q-gram，计算出散列值，找到对应的倒排索引，并在该索引末端加入当前行号。如果输入字串有重复的Q-gram，那么当前行号可能会在倒排索引中插入多次。然后窗口向右移动一格，把之前的散列值通过rolling hash计算出下一时刻的值。

输入文件读入完毕后，对于hash table中的每个倒排索引(必然是非空的)，在末端加入作为哨兵元素的无穷大。

Filter

对于一个查询，使用类似构建索引时的Rabin-Karp string search algorithm，对于每个长为的窗口中的Q-gram，找到对应的倒排索引，把指向首元素的指针放入列表中。设查询字串长度位，那么中将会有个指针(可能重复)。

建立binary heap

列表的元素是指向倒排索引的指针，以指针指向的值为关键字使用Floyd’s algorithm 在时间内建立binary heap 。

Tournament sort进行N-way merge

1. 堆顶指针指向的值为，若old为无穷大则返回

2. 计算堆顶元素指向的值的出现次数，若大于等于阈值则添加到候选集中

3. 把堆顶元素指针向前移动一格(即指向对应的倒排索引的下一项)，若下一项仍等于原来指向的值则继续移动

4. 上述操作后堆顶指针指向的值变大了，对它进行下滤操作

5. 若新的堆顶指向的值等于则跳转到步骤3

之后对候选集的每个元素进行检验，是否满足Jaccard index或Levenshtein编辑距离的阈值要求， 输出筛选后的。

1. 使用启发函数把倒排索引划分为长索引和短索引两类，长索引有个，其中为索引个数

2. 对短索引采用MergeSkip算法，对于短索引中所有出现次数不少于的元素，在所有长索引中二分检索

3. 将出现次数不少于的元素添加到候选集中

4. 把堆顶元素指针向前移动一格(即指向对应的倒排索引的下一项)，若下一项仍等于原来指向的值则继续移动

5. 上述操作后堆顶指针指向的值变大了，对它进行下滤操作

6. 若新的堆顶指向的值等于则跳转到步骤4

7. 从堆中弹出个元素，使用二分检索把这些倒排索引指针移动至大于当前堆顶指向的值，再重新插入堆中

Verification

Levenshtein edit distance

需要对每个候选字串和查询字串计算编辑距离。

两个字符串的Levenshtein edit distance可以使用的Needleman–Wunsch algorithm计算。

注意到代码中使用到编辑距离的地方都有阈值限制，如果编辑距离超过阈值，那么它的实际值无关紧要。因此我们可以只计算动态规划矩阵中对角线带状区域的状态。

另外当其中某个字符串的长度小于等于128时，还可以采用bit vector的算法@edit03加速到。

两个字符串的Levenshtein edit distance的下界是字符集所有字符出现频数差的绝对值的和的一半，当该下界小于等于阈值时再进行实际计算。可以用_mm_sad_epu8来估算频数差的绝对值的和。当某个字符频数差大于等于256时会低估实际值，但对结果没有影响。

Jaccard index

采用scan count的方式。 先用rolling hash计算查询串所有Q-gram的标号，在计数容器中增加一。然后对于候选串的所有Q-gram，若计数容器中的值大于零则减去零并加到答案中。再便利候选串的所有Q-gram，把减去的值再加回来。

ppjoin@ppjoin

之前一个疑惑是没理解similarity join和执行若干次similarity search有什么区别。 原来是similarity search构建的索引能支持阈值不同的查询，而similarity join直接指定了固定阈值， 因此构建的索引可以利用这个性质。

Prefix filtering

按照一个全序排序entity包含的gram，那么若两个串的overlap满足：，则的前个q-gram必然与的前个gram有交集。

Jaccard index转化为overlap

由可得。

另由$ J(x,y) t |x| t |y|$

如果需要能所探寻到所有overlap超过的的串，取前缀长度为即可。

论文中没有提及某gram被同一个entity包含多次的情况。这时的前缀和的前缀的交集大小似乎不能有效地精确计算出来。

ppjoin

对于查询串，计算，探测前个gram的倒排索引后得到一些候选entity，并且知道每个候选entity 的前个gram和前个gram的交集大小，如果加上后不到下界，则可以剔除。

需要一种类似数组的数据结构支持三种操作：清零、访问某一项、列出上次清零以来所有访问过的项。可以用三个数组和一个计数器实现。

Positional filtering

根据overlap计算hamming distance上界后根据和的某几个对应的相等字符估算hamming distance下界，判断是否可行。

当gram有重复时比较麻烦，SuffixFilterWeighted中不能直接用mid作为的枢轴，需要取 中第一个取值和mid相同的字符。

对于可能重复的gram，另一种处理方式是让各gram取不同的值。

Approximate entity extraction

任务

实现近似抽取，近似串有两种度量方式：Levenshtein edit distance和Jaccard index。 需要实现AEE类的createIndex、aeeED、aeeJaccard三个方法。

Faerie algorithm

实现采用@faerie中提到的Faerie algorithm。

索引

读入描述entity的文件采用mmap：

struct stat s;
int fd = open(filename, O_RDONLY); fstat(fd, &s);
mmap(0, s.st_size, PROT_READ, MAP_PRIVATE | MAP_POPULATE, fd, 0);

其中的MAP_POPULATE是为了让产生read-ahead的效果，加速文件读入。

索引的数据结构包含：

• entity向量e

• 把Q-gram映射为entity编号的若干倒排索引s2gid。

• 若干倒排索引gid2e，为每个entity中出现的Q-gram保存包含该Q-gram的entity向量。

对于每个输入的字串，使用类似Rabin-Karp string search算法的方式，获取当前长为的窗口中的Q-gram，计算出散列值，找到对应的倒排索引，并在该索引末端加入当前行号。如果输入字串有重复的Q-gram，那么当前行号可能会在倒排索引中插入多次。然后窗口向右移动一格，把之前的散列值通过rolling hash计算出下一时刻的值。

s2gid的每个倒排索引末尾添加哨兵元素INT_MAX。

近似抽取

Levenshtein edit distance和Jaccard index均可用Faerie算法处理。对于每个文档执行一次single-heap based algorithm。

建立binary heap

首先把长度为的doc划分为的Q-gram，经s2gid映射后得到个指向倒排索引的指针。以指针指向的值(entity编号)为第一关键字，位置为第二关键字使用Floyd’s algorithm在时间内建立binary heap L。

Tournament sort进行N-way merge得到候选子串

令表示entity 的长度(和论文中定义不同)。

如果是Levenshtein edit distance查询，则设置， ，； 如果是Jaccard index查询，则设置， ，。

1. 记堆顶元素为eeid，弹出所有等于eeid的元素得到@faerie中的。

2. 由于位置为第二关键字，得到的以及有序了。

3. 使用尺取法寻找包含中至少个元素，且包含的Q-gram数在区间内的所有窗口。

4. 每个窗口可以产生若干候选子串。

代码使用了batch-count pruning，使用尺取法时可以用@faerie中提到的二分检索方法，一次把指针移动若干步。

Verification

之后对每个候选子串进行检验，是否满足Jaccard index或Levenshtein编辑距离的阈值要求。

Levenshtein edit distance

两个字符串的Levenshtein edit distance可以使用的Needleman–Wunsch algorithm计算。

注意到代码中使用到编辑距离的地方都有阈值的限制，如果编辑距离超过阈值，那么它的实际值无关紧要。因此我们可以只计算动态规划矩阵中对角线带状区域的状态。

另外当其中某个字符串的长度小于等于128时，可以使用内置类型__int128采用bit vector的算法@edit03加速到。

两个字符串的Levenshtein edit distance的下界是字符集所有字符出现频数差的绝对值的和的一半，当该下界小于等于阈值时再进行实际计算。可以用_mm_sad_epu8来估算频数差的绝对值的和。当某个字符频数差大于等于256时会低估实际值，但对结果没有影响。

Jaccard index

计算两个串和的Jaccard index时使用公式。

采用scan count的方式计算。根据s2gid计算查询串所有Q-gram的编号，在计数容器中增加一。然后对于候选串的所有Q-gram，若计数容器中的值大于零则减去零并加到答案中。再遍历候选串的所有Q-gram，把减去的值再加回来。

Trie-based@taste

令Levenshtein编辑距离阈值为，对于每个entity ，划分为个片段存入trie。

若文档和某个相似，则文档必然以的某个片段为子串。检索trie即可得到所有候选entity。

当探测到文档的某子串对应的trie节点包含某个entity ，则就是一个候选entity，且可以知道 的某个已经出现在中了，包含的某个更长子串和的编辑距离是：

即需要把前面的部分和匹配，后面的部分和匹配，两部分可以分开考虑。总的编辑距离就是两部分匹配结果编辑距离的和。如果左侧的，则右侧的最大可以是。

可以用带阈值限制的编辑距离算法计算。

多个串共同包含时复用计算结果

多个串共同包含时，它们的右侧部分可能也有公共前缀，这部分串的编辑距离结果可以复用。

把trie节点中检索到的entity按组织为下层trie(原trie为上层trie)。求出下层trie的最左叶节点和的编辑距离后，要切换到次左叶节点，它们的longest common prefix和的编辑距离动态规划值可以复用。

构建下层trie比较耗空间，可以借鉴suffix array的思路，把索引到的entity的右侧部分排序，先计算字典需最小和的编辑距离，再计算字典序次小的和的编辑距离，如此处理其他所有。

另外如果发现计算到时发现所有都超过了，那么可以立刻停止计算。

生成结果

把匹配某个左侧部分的和匹配对应右侧部分的求cartesian product，如果两部分编辑距离和小于，拼接两部分以及可以得到一个结果子串。

文档的某个子串和某个的公共部分可能较长，导致的多个片段都在trie中被检索到。产生的结果可能会重复，另外编辑距离的计算各片段间也会有很大的重叠。我没想到怎么利用。

Aho-Corasick automaton

目前的方式是对于文档的每个位置都对上层trie探测得到候选entity，可以Aho-Corasick automaton改进。 注意Aho-Corasick automaton和Aho-Corasick algorithm的区别，前者会把trie改造为图(一些网络资料称之为trie图)。探测的文档子串的右边界在不断增加，左边界要根据Aho-Corasick状态的转移选择性变化。

TrieNode *p = trie_root, *q; for (int i, j = 0; j < m; ) {
  u8 c = doc[j++];
  i += p->dep+1-p->ch[c]->dep;
  p = p->ch[c];
  for (ii = i, q = p; ; ) {
    // 考虑文档d[ii,j)和节点q表示的e_m的下层trie q->inferior
    if (p->pi) {
      ii += p->depth-p->pi->depth;
      p = p->pi;
    } else
      break;
  }
}

对于每个匹配的p都要沿着p->pi->pi->…炼上溯到根。可以对于每个trie节点记录其最长的表示一个的后缀(即pi的若干次幂)。这样可以被多串匹配部分的复杂度从优化到，其中为文档长度，为出现次数和，为单个的长度。

演化

Faerie 7.263 Faerie+ED共用 4.197 Trie-based初版 2.4s 使用Aho-Corasick automaton后2.264s 利用公共前缀后 2.133s

实现空间数据库的即敲即得式检索系统

实验要求

• 实现空间数据库的即敲即得式检索系统

• 给定100w个POI，以及一个查询，找到所有的相关结果

• 基于位置的检索和即敲即得式检索

运行方式

项目由两部分组成，实现检索算法的部分为后端，由C++11编写； Web展示部分由网页前端和Ruby Sinatra写的web服务器组成。

运行后端：

g++ -std=c++11 -O3 src/a.cc -ljsoncpp -o a
./a

将会读取当前目录下的zipcode.json并监听TCP 1337端口。

运行web服务器：

ruby web/web.rb

将会监听0.0.0.0:4567。

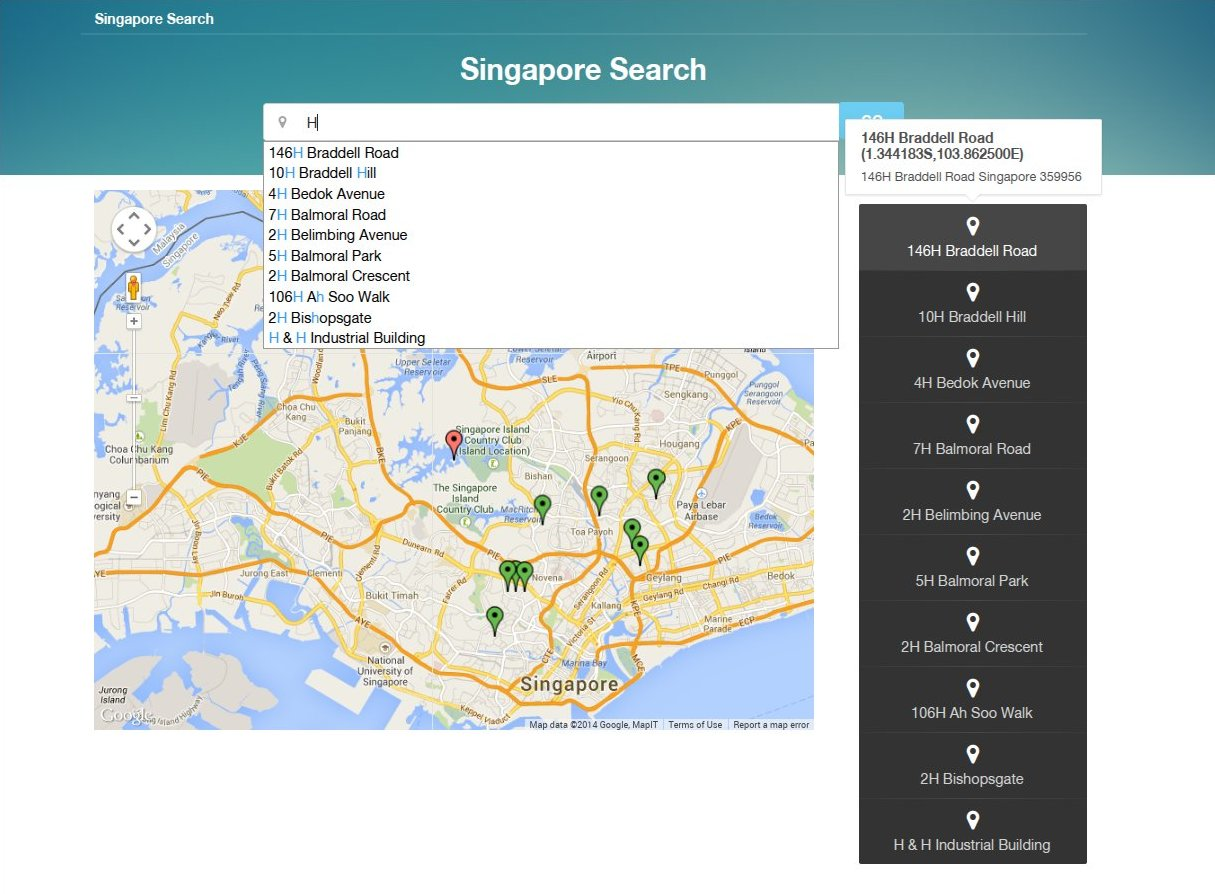
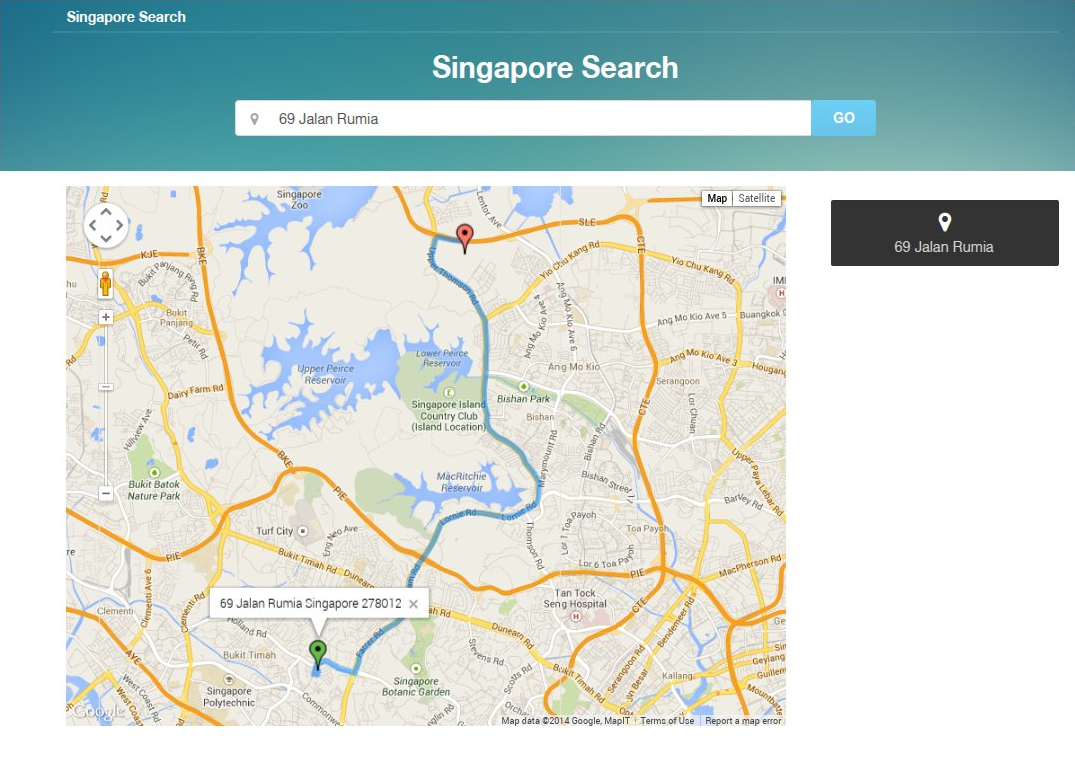
使用说明

浏览器打开，在输入框中填写字串，点击地图上某处作为起点，就会用marker的方式显示最近10个地点，且name 字段包含字串。

点击marker或者代表候选地点的右侧按钮， 即可显示起点到该地点的路径。

项目实现

JSON输入文件处理

输入文件为JSON格式的zipcode-address.json，后端程序使用C++库JsonCpp进行JSON的解析和渲染。

位置检索

根据实验要求，location-aware instant search的方法直观上是最适合的。但考虑到数据规模和prefix-region tree的描述，及想要实现任意子串而非单单前缀的查询，我在项目中分别实现了位置检索和地名检索。

位置检索属于multidimensional spatial data structure的应用。考虑到我们需要处理的询问：求出矩形区域内的地点和与给定点最近的k个地点，解决这类问题最常用的数据结构是R-tree家族。

R-tree

R-tree是派生于B+-tree的层次化数据结构，存储d维点或矩形，一般的物体可以转化为最小包围盒后用矩形的方式存储。 R-tree除根以外的节点度限制为，其中，叶节点存储若干物体，以及这些物体的最小包围盒，内部节点存储其包含的所有节点的包围盒的最小包围盒。

R-tree的操作通常用自顶向下遍历，根据查询和包围盒的相关性来剪枝。 R-tree的缺点是分解是数据相关的，很难进行集合论操作比如交集。

Bulk loading

很多应用数据是静态的，或者修改不频繁，即使是动态的也很有可能很多数据可以提前知道。这时一次插入一项会带来较大的加载代价，空间利用也不充分，结构不够好。此时进行根据输入数据特点进行bulk loading即建立初始数据结构是比较好的选择。

R-tree bulk loading的通用的算法是：

1. 把矩形划分为个分组，每个分组为一个叶节点。最后一个分组分配到的矩形可能不到个。

2. 递归地把若干个节点合并为一个上一层的大节点，直到根节点被创建。

一种比较好的启发式合并算法是Sort-Tile-Recursive。

Priority R-tree

@prtree是一种R-tree变体，window query的时间复杂度为，是第一个达到该最坏情况下渐进最优复杂度的R-tree变体。

PR tree的起源，其中Priority R-tree诞生年份应为2004年

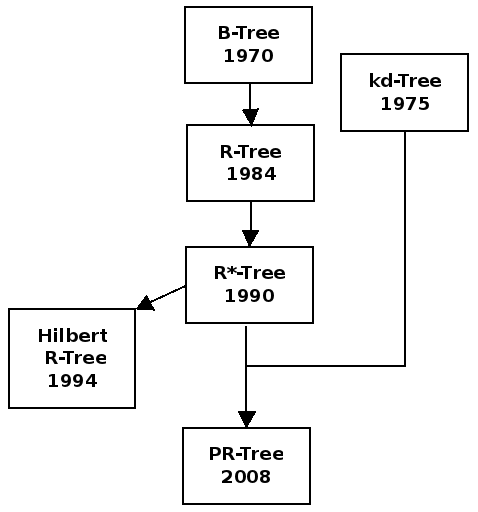
Priority R-tree算法实际上指的是R-tree的一种bulk loading算法。 Priority R-tree的构建为若干次pseudo priority R-tree构建过程。

Pseudo priority R-tree的构建方式如下：

Extract B left-extreme points. Store them in a leaf-node.
Extract B bottom-extreme points. Store them in a leaf-node.
Extract B right-extreme points. Store them in a leaf-node.
Extract B top-extreme points. Store them in a leaf-node.
Partition the remaining n - 4B nodes into two halves based on our current tree depth, using the same scheme as found in the kd-tree data structure:
If ((depth % 4) == 0) partition by the x-coordinate (left-extreme).
If ((depth % 4) == 1) partition by the y-coordinate (bottom-extreme).
If ((depth % 4) == 2) partition by the x-coordinate in reverse (right-extreme).
If ((depth % 4) == 3) partition by the y-coordinate in reverse (top-extreme).
Recursivly apply this algorithm to create two sub-trees on the partitioned halves.
Stop when no points remain to be indexed (e.g. stop when n - 4B ≤ 0).

去除pseudo priority R-tree的内部节点，把叶节点看作物体继续调用pseudo priority R-tree进行下一轮构建，得到的内部节点再进行构建，如此反复直到叶节点数，之后创建一个根节点包含所有叶节点。

我的实现参考了一个Java版的priority R-tree实现：https://github.com/dshanley/prtree。

K-nearest neighbors

采用best-first search实现k-nearest neighbors问题，以距离的下界作为估价函数。

地名检索

C++后端实现了给出一个字串，输出所有包含该字串的地点的功能。这个需求可以转化为string search问题。

Suffix array构建

Suffix array是解决string search问题的一个工具，它是一个字串所有后缀的排序。

线性时间的构建算法主要有Kärkkäinen-Sanders(@dc3)、Ko-Aluru(@ka)、KSP三种，其中KSP算法使用了类似suffix tree的构建方式， Kärkkäinen-Sanders算法时间复杂度的递推式为，通常认为性能不如的Ko-Aluru。

项目中我实现了Ko-Aluru算法，并按照@yangzhe的注记，借鉴@nzc对LMS substring递归排序使用的方法，对原始的Ko-Aluru算法进行改动以简化内存使用和提升性能。我的实现在字串和suffix array外仅使用两个数组：计数排序使用的桶和一个表示L/S类型的数组，反映了Ko-Aluru算法能达到和@nzc同等的精简内存占用。

Ka-Aluru suffix array construction algorithm

规定为哨兵字符，且小于字符集中任意一个字符。对于字串个每个后缀，根据和的大小关系得到后缀的类型，然后根据把所有后缀分为两类：

令字符集为，再根据后缀首字母分类：

并结合以上两种分类定义：

对于，中的后缀排在中后缀的前面，因为如果两个后缀和的第一个字符、不同，那么和的大小关系可以直接确定。另外中的后缀排在中后缀的前面，因为中后缀均小于，而中后缀均大于。

Suffix array即为。

根据@ka的induced sorting，只要确定了的大小顺序，那么的顺序也可以确定。同样地，只要确定了的大小顺序，那么的顺序也可以确定。根据抽屉原理或有一个，不妨设，只要求出中所有后缀的大小顺序，那么使用induced sorting即可得到的大小顺序。再根据中的后缀排在中后缀的前面，即可得到所有后缀的大小顺序。

下面考虑如何递归求出的大小顺序。@ka使用了一个复杂的方法，根据-distance计算。借鉴@nzc对LMS substring递归排序使用的方法，我在实现中使用了一个简单的方法。定义^--substring为夹在相邻两个^-类型字符间的子串。定义一个^--substring 小于另一个^--substring 当且仅当字典序小于，其中两种取值规定^-小于⁺。

对于两个长度不同的^--substring 和，它们不会相等，且根据^--substring的大小关系可以得到和的大小关系。如果两^--substring相等，找到在原串后的^--substring ，两者共用一个字符。再找到在原串后的^--substring ， 和的大小关系即为和的大小关系。如果这两个子串也相同了，那么可以继续找紧接着的下一对^--substring。

根据以上比较方式可以发现如果取出中所有^--substring，并把这些^--substring看作字符，就可以得到子问题递归调用算法解决。现在考虑如何确定所有^--substring的大小关系，使得长度不同的可以区分大小，而长度相同的允许相等(所以才需要递归确定大小)。

先用桶排序求出所有^-类型字符的大小，使用一次induced sorting根据^-计算 ⁺，这样便得到了所有形如子串的大小。再用一次induced sorting根据⁺计算^-，便得到了所有形如类型子串的大小，而这些串就是我们需要的^--substring。

对^--substring计算新字符集大小，若小于^--substring数目则说明所有 ^--substring的顺序已经确定，否则取出^-字符递归计算suffix array。得到这些^--substring的顺序即的顺序后使用induced sorting即可得到整个suffix array。

实现技巧

为原串，为类型数组，为桶排序使用的桶。

整个实现分为几个阶段，仍然设：

1. 计算数组，需要使用

2. 使用两次induced sorting计算^--substring的大小，需要使用

3. 根据^--substring构建新字串递归计算子suffix array

4. 根据子suffix array计算部分的suffix array

5. 使用induced sorting根据部分的suffix array得到整体suffix array

其中第2、3步需要特别使用了很多技巧节省空间占用。

注意到，因此新字串和子suffix array的空间占用和，可以让它们共用 原始的suffix array的空间。这样根据子suffix array计算部分的suffix array的过程变成了把suffix array扩张的过程，而扩张时需要根据新字串和的字符对应关系的映射进行，因为映射的性质可以共用一个数组实现，扩张中suffix array储存了三部分的内容：映射、子suffix array、部分的suffix array， 其中部分的suffix array渐渐变大，子suffix array渐渐变小。 求得部分的suffix array后，原地桶排序得到原始下标的。

递归也需要使用数组，因为计算是线性的，可以让递归时继续使用该数组，递归函数返回时重新计算被覆盖的部分。这样可以省去数组在递归中不断被创建的开销。

多数文献都在末尾添加哨兵元素以方便讲解，但个人感觉实现中哨兵元素通常会导致更复杂的判断，弊大于利。不使用哨兵元素只需要在三个地方注意，

• 为^-，因为把哨兵字符看作字典序最小。

• 根据⁺-substring计算^--substring的induced sorting过程提前把放入桶中。 否则因为它是最后一个字符，无法被放入桶中，当该字符的桶包含两个或更多元素时可能会导致它的位置被覆盖而出错。

• 计算新字符集时，需要注意比较过程中到达边界的情况。

使用suffix array检索字串

把所有地点的名字拼接为一个字串后检索字串的问题就转化为找到所有包含该字串的位置。在suffix array中检索所有长为的可以使用二分检索在时间内得到：

def search(P):
    l = 0; r = n
    while l < r:
        mid = (l+r) / 2
        if P > A[mid]:
            l = mid + 1
        else:
            r = mid
    s = l; r = n
    while l < r:
        mid = (l+r) / 2
        if P < A[mid]:
            r = mid
        else:
            l = mid + 1
    return (s, r)

String search可以用suffix tree的top-down traversal轻易实现。 @sa04提出了使用lcp表增强suffix array的功能，从而实现时间检索。给suffix array扩充lcp表后suffix array即能实现suffix tree的top-down traversal功能。

childtab

-interval 定义为：

其性质是后缀的LCP为。

满足的称为-interval 的-index。这些-index把划分为若干子区间，每个子区间可能是单元素区间，或者是LCP更大的-interval()。

根据这些-interval的包含关系构建一棵以-interval为节点的树，就得到了没有叶节点的suffix tree。

\begin{aligned}
  \text{up}[i] &=& \min{\{ q \in [0,i) | \text{lcp}[q] > \text{lcp}[i] \text{ and } \forall k\in [q+1,i): \text{lcp}[k]\geq \text{lcp}[q]\}} \\
  \text{down}[i] &=& \min{\{ q \in [i+1,n) | \text{lcp}[q] > \text{lcp}[i] \text{ and } \forall k\in [i+1,q): \text{lcp}[k] > \text{lcp}[q]\}} \\
  \text{next}[i] &=& \min{\{ q \in [i+1,n) | \text{lcp}[q] = \text{lcp}[i] \text{ and } \forall k\in [i+1,q): \text{lcp}[k] > \text{lcp}[i]\}} \\\end{aligned}

可以这样计算：

last = -1
push(0)
for i = [1,n)
  while lcp[i] < lcp[top]
    last = pop
    if lcp[i] <= lcp[top] && lcp[st] != lcp[last]
      down[top] = last
  if last != -1
    up[i] = last
    last = -1
  push(i)
while 0 < lcp[top]
  last = pop
  if lcp[top] != lcp[last]
    down[top] = last
if last != -1
  up[n] = last

push(0)
for i = [1,n)
  while lcp[i] < lcp[top]
    pop
  if lcp[i] == lcp[top]
    next[top] = i
    pop
  push(i)

有些项没有值，不妨设为无效值。

用一个数组child表示

如果有效，则，推出和都无效。

对于一个可分割的-interval ，，令，则为各个子区间的分割点。因此可以记录在和数组中。

进一步，有多个区间终点相同，它们计算子区间要用到。令该值为最大的区间的值，则其他较小区间的分割点都必须用左边界的值计算，而这些较小区间都是其父区间的最后一个子区间，所以它们的左边界的值都为，刚好可以用来存储。这样，三个数组可以只用一个数组存储。

其中、和可以这样区分：

• 表示：-1 < child[i] && child[i] <= i

• 表示：child[i] > i && lcp[child[i]] > lcp[i]

• 表示：child[i] > i && lcp[child[i]] == lcp[i]

比如要在suffix array中搜索needle，@sa04中的伪代码没有考虑越界，修正如下：

found = true
(l, h) = get_interval(0, n, s[0])
i = 1
while found && i < m
  if l < h-1
    j = min(get_lcp(l, h), m)
    found = a[sa[l]+i...sa[l]+j] == needle[i...j]
    i = j
    if i < m
      (l,h) = get_interval(l, h, s[i])
  else
    found = a[sa[l]+i...sa[l]+m] == needle[i...m]
    i = m
return found ? (l, h) : (-1, -1)

如果要输出方案，那么复杂度变为，其中是出现的次数。

得到包含needle的区间后，根据rank得到原字符串中的位置，即可知道哪些地点包含该字串。

结果呈现

前端

前端使用Slim作为HTML的模板引擎，Sass为CSS预处理器，CoffeeScript为JavaScript预处理器，使用Semantic-UI CSS框架。Model和view的绑定采用了Model View ViewModel设计模式的 knockout.js。

Web服务器

项目中实现了基于Ruby的Sinatra实现了一个web server：web/web.rb。

对于地图点击，前端将用ajax向web服务器提交请求，web/web.rb收到查询请求后会使用TCP socket向后端的C++服务器发送请求， C++服务器进行位置检索，web服务器得到应答后以JSON格式发送给前端，前端再进行处理。

自动补全的实现方式类似。前端的jquery-autocomplete发现输入框内容改变后向web服务器提交ajax请求，web/web.rb收到查询请求后使用TCP socket向后端的C++服务器发送请求，C++服务器使用suffix array进行地名检索。

结果展示

搜索框的自动补全是用jquery-autocomplete发送ajax请求由后台返回的

使用Google Directions API计算路线