计算机系统结构

存储层次分析及程序优化

测试环境

系统

使用的机器CPU为Intel(R) Core(TM) i5-3317U CPU @ 1.70GHz，可以在cpu-world.com上查到各级cache大小，L1 data cache为32KiB，L2 cache为256KiB，L3 cache为3072KiB。

编译器

% gcc -v
Using built-in specs.
COLLECT_GCC=/usr/x86_64-pc-linux-gnu/gcc-bin/4.8.2/gcc
COLLECT_LTO_WRAPPER=/usr/libexec/gcc/x86_64-pc-linux-gnu/4.8.2/lto-wrapper
Target: x86_64-pc-linux-gnu
Configured with: /var/tmp/portage/sys-devel/gcc-4.8.2-r1/work/gcc-4.8.2/configure --host=x86_64-pc-linux-gnu --build=x86_64-pc-linux-gnu --prefix=/usr --bindir=/usr/x86_64-pc-linux-gnu/gcc-bin/4.8.2 --includedir=/usr/lib/gcc/x86_64-pc-linux-gnu/4.8.2/include --datadir=/usr/share/gcc-data/x86_64-pc-linux-gnu/4.8.2 --mandir=/usr/share/gcc-data/x86_64-pc-linux-gnu/4.8.2/man --infodir=/usr/share/gcc-data/x86_64-pc-linux-gnu/4.8.2/info --with-gxx-include-dir=/usr/lib/gcc/x86_64-pc-linux-gnu/4.8.2/include/g++-v4 --with-python-dir=/share/gcc-data/x86_64-pc-linux-gnu/4.8.2/python --enable-languages=c,c++,fortran --enable-obsolete --enable-secureplt --disable-werror --with-system-zlib --enable-nls --without-included-gettext --enable-checking=release --with-bugurl=https://bugs.gentoo.org/ --with-pkgversion='Gentoo 4.8.2-r1 p1.4-ssptest, pie-0.5.9-ssptest' --enable-libstdcxx-time --enable-shared --enable-threads=posix --enable-__cxa_atexit --enable-clocale=gnu --enable-multilib --with-multilib-list=m32,m64 --disable-altivec --disable-fixed-point --enable-targets=all --disable-libgcj --enable-libgomp --disable-libmudflap --disable-libssp --enable-lto --without-cloog
Thread model: posix
gcc version 4.8.2 (Gentoo 4.8.2-r1 p1.4-ssptest, pie-0.5.9-ssptest)

编译选项为：export CXXFLAGS=’-std=c++11 -g -O3 -march=native’

查看cache信息也可以使用如下方法：

sysconf

获取L1 cache line大小：

% getconf LEVEL1_DCACHE_LINESIZE
64

dmidecode

查看系统的DMI信息，可以发现两个32K的L1 cache分别是数据cache和指令cache。

L1 data cache的相连度为8，大小为32KiB。

L2 cache的相连度为8，大小为256KiB。

% sudo dmidecode -t cache
# dmidecode 2.12
SMBIOS 2.7 present.

Handle 0x0005, DMI type 7, 19 bytes
Cache Information
        Socket Designation: L1 Cache
        Configuration: Enabled, Not Socketed, Level 1
        Operational Mode: Write Through
        Location: Internal
        Installed Size: 32 kB
        Maximum Size: 32 kB
        Supported SRAM Types:
                Unknown
        Installed SRAM Type: Unknown
        Speed: Unknown
        Error Correction Type: Parity
        System Type: Data
        Associativity: 8-way Set-associative

Handle 0x0006, DMI type 7, 19 bytes
Cache Information
        Socket Designation: L1 Cache
        Configuration: Enabled, Not Socketed, Level 1
        Operational Mode: Write Through
        Location: Internal
        Installed Size: 32 kB
        Maximum Size: 32 kB
        Supported SRAM Types:
                Unknown
        Installed SRAM Type: Unknown
        Speed: Unknown
        Error Correction Type: Parity
        System Type: Instruction
        Associativity: 8-way Set-associative

Handle 0x0007, DMI type 7, 19 bytes
Cache Information
        Socket Designation: L2 Cache
        Configuration: Enabled, Not Socketed, Level 2
        Operational Mode: Write Through
        Location: Internal
        Installed Size: 256 kB
        Maximum Size: 256 kB
        Supported SRAM Types:
                Unknown
        Installed SRAM Type: Unknown
        Speed: Unknown
        Error Correction Type: Multi-bit ECC
        System Type: Unified
        Associativity: 8-way Set-associative

Handle 0x0008, DMI type 7, 19 bytes
Cache Information
        Socket Designation: L3 Cache
        Configuration: Enabled, Not Socketed, Level 3
        Operational Mode: Write Back
        Location: Internal
        Installed Size: 3072 kB
        Maximum Size: 3072 kB
        Supported SRAM Types:
                Unknown
        Installed SRAM Type: Unknown
        Speed: Unknown
        Error Correction Type: Multi-bit ECC
        System Type: Unified
        Associativity: 12-way Set-associative

sysfs

另外也可以查看sysfs：

% for i in /sys/devices/system/cpu/cpu0/cache/*; do echo -- $i; cat $i/{type,size,ways_of_associativity}; done
-- /sys/devices/system/cpu/cpu0/cache/index0
Data
32K
8
-- /sys/devices/system/cpu/cpu0/cache/index1
Instruction
32K
8
-- /sys/devices/system/cpu/cpu0/cache/index2
Unified
256K
8
-- /sys/devices/system/cpu/cpu0/cache/index3
Unified
3072K
12

测量方法

步长均以字节为单位。

分配一个大小和测试项目有关的数组，以特定步长顺序访问，访问完后从首元素开始继续访问(即循环顺序访问)。

双层循环

其中一种实现方式是内外两层循环，内循环执行次数和数组大小与步长相关，外循环执行次数根据内循环执行次数计算得到，控制访问总次数固定。代码如下：

1
2
3
4
5
int a[...], k;
REP(i, total/size)
  for (unsigned j = 0; j < size; j += stride)
    k = a[j];
volatile int z = k;

其中volatile是为了保证向z的存储位置写入值，从而防止k的计算被优化掉。

单循环，两个循环变量

上面方法的问题在于对于不同的数组大小和步长，内循环执行次数不同。在固定循环次数的情况下，内循环较大的效率略高。为了减少干扰，我们应该尽量使用单循环。

我们可以使用一个变量控制循环次数，另一个变量控制访问的数组索引。考虑到测试的数组大小、步长等都是2的幂，可以使用位与把数组索引限制在有效范围内：

1
2
for (unsigned j = 0, i = ITERS; i > 0; j += s, i--)
  a[j & mask]++;

其中mask是数组大小减一

使用1-tree设计仅含三条汇编指令的单循环

如果把数组元素设想为节点，值看作索引作为指向其他元素的指针，数组可以看作是多个1-tree形成的pseudoforest。比如设计这样一个包含0的1-tree：，即a[0]==16, a[16]==32, ..., a[96]==0。 按如下方式设计循环体：

1
2
3
4
int k = 0;
for (unsigned j = ITERS; j; j--)
  k = a[k];
volatile int z = k;

g++ -O3编译可以发现得到了如下指令：

  401240:   83 e8 01                sub    eax,0x1
  401243:   8b 14 91                mov    edx,DWORD PTR [rcx+rdx*4]
  401246:   75 f8                   jne    401240 <_Z10cache_sizev+0x1d0>

仅包含三条指令。 如果把cache miss的代价视为常数，那么尽量减少每轮迭代里其他开销可以凸显cache miss的损失。

在测量cache大小时发现采用这种循环方式确实cache miss显示得更清楚了，但是L2 cache的miss就不明显了：

image

另外索引的变化方式似乎变得不易预测了，效率变低了一些。

其他

数组按照L2 cache大小和页大小的倍数对齐比较好。

可以使用aligned_alloc或posix_memalign等函数，代码中按4MiB对齐。

另外数组分配完后，在测试前需要修改各页以防止demand paging对测量结果造成影响。

Cache大小测量

策略

数组大小从4KiB开始翻倍，每次间隔16个元素顺序访问，测量重复若干次的访问时间。

设计原理

顺序访问两倍cache大小的数组会导致任何cache替换策略都全部miss。数组大小每次都扩大一倍看访问时间，当时间突然增加时就表示当前的数组大小已经超过目前考察的某层次cache的大小了。

因为hardware prefetching@prefetch的存在，数组访问的索引步长不能太小。另外固定数组访问次数测评时，如果索引步长较小，那么cache miss的比例也会降低，使得相应的损失不够显著。

实验结果

源文件为src/a.cc

% ./a -c
stride(KB)      time(s)
4               0.508398
8               0.494066
16              0.506885
32              0.504679
64              1.059095
128             1.077871
256             1.141273
512             1.422013
1024            1.447682
2048            1.694575
4096            3.108610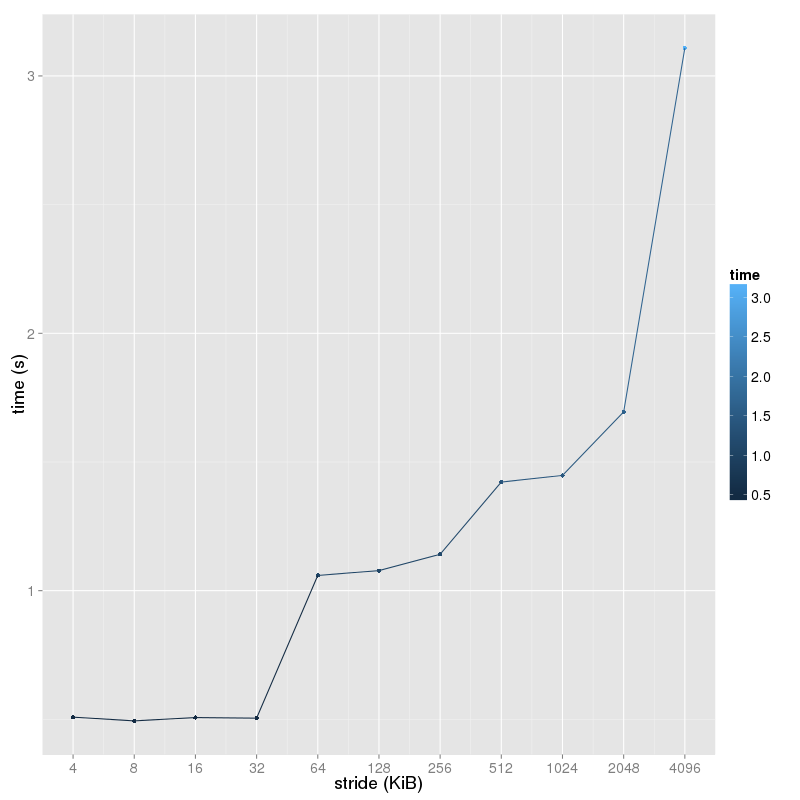
image

实验数据分析

可以看出来在32KiB升64KiB、256KiB升512KiB、2048KiB升4096KiB处运行时间有较大的增幅，印证了L1 data cache为32KiB，L2 cache为256KiB，L3 cache在2048KiB和4096KiB之间。

代码中我取stride为256，实际测试发现当stride为32时将无法发现32KiB升64KiB时的较大增幅，可能是因为hardware prefetching的存在， 硬件检测到了内存访问的模式而进行了预存。

另一种策略

根据@cs519，上述方法采用了capacity miss的性质来测量cache大小，另外可以使用conflict miss。 类似于cache line大小的测量，当以cache size为步长大小或更大的步长访问时， 冲突会比较大，导致性能下降。

代码中的cache_size_alternative实现了该方法，但未能印证cache大小。

Cache块大小测量

策略

考察L1 cache时，数组大小设为L1 cache大小的两倍，以特定步长访问数组。每次把步长倍增，当发现运行时间有较大增幅时表明步长已经大于等于cache line大小。

之后再把数组大小设为L2 cache两倍，做类似的测试。虽然L1 cache包含在L2 cache里，但因为比L2 cache小很多，造成的影响小于L2 cache miss的影响。所以如果L2 cache的块大小不同，应该能看到另一处也有阶梯状现象。

设计原理

数组大小为两倍cache大小时，cache line会被不停地替换掉。一个cache line可能可以容纳多个元素，只有该cache line的第一次元素访问才会miss，有较大代价， 之后的访问会变快。当后每次访问都会miss，步长增大也不会使时间进一步提高。

实验结果

% ./a -l 65536
stride(B)       time(s)
4               0.254627
8               0.250141
16              0.252348
32              0.288567
64              0.532215
128             0.531537
256             0.529876
512             0.534260

% ./a -l 262144
stride(B)       time(s)
4               0.252893
8               0.254049
16              0.256715
32              0.295765
64              0.591509
128             0.595276
256             0.586291
512             0.582670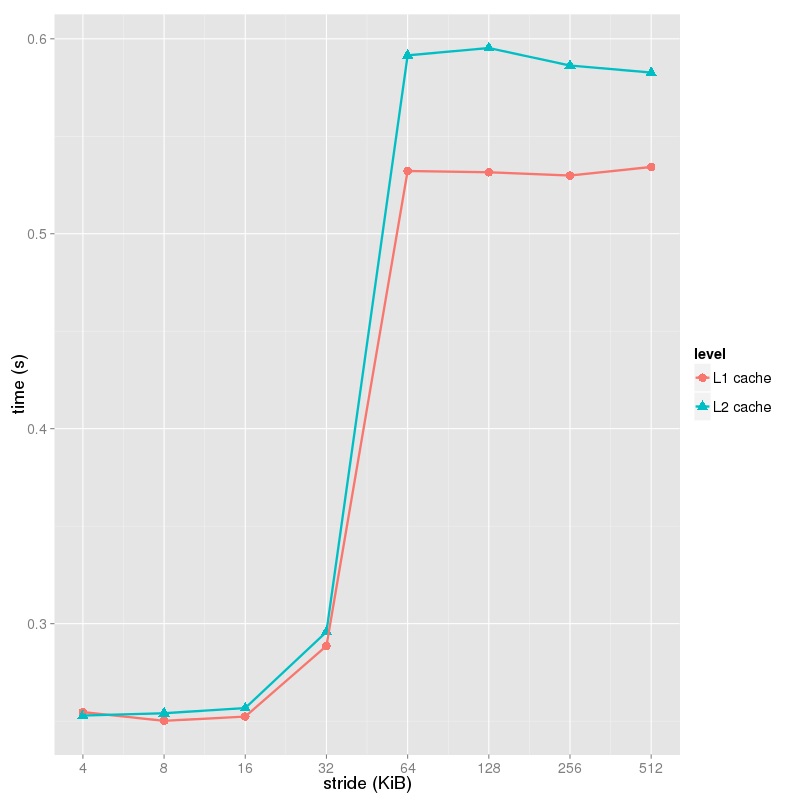
image

实验数据分析

对64KiB的L1 cache大小，可以看到步长为64时时间有较大增长，但之后趋于平稳，故cache line大小为64字节。

对256KiB的L2 cache大小，可以看到步长为64时时间有较大增长，但之后趋于平稳，故cache line大小为64字节。

Cache相连度

策略

数组大小设置为cache大小，然后每次倍增，以cache大小为步长访问，当一个循环内访问的元素数大于等于set-associativity的两倍时，上一次枚举的ways就是set-associativity。

设计原理

以cache大小为步长访问时，每次访问的元素的索引值都相同。当访问的元素数大于等于set-associativity的两倍时，就会保证每次访问都会miss，从而时性能急剧下降，且上一次枚举的ways就是所求。

实验结果

% ./a -a $[32*1024]
ways    time(s)
1       0.670270
2       0.669508
4       0.674767
8       0.673887
16      0.846521
32      1.409794

% ./a -a $[256*1024]
ways    time(s)
1       0.670007
2       0.665101
4       0.670972
8       0.643787
16      2.684241
32      7.747577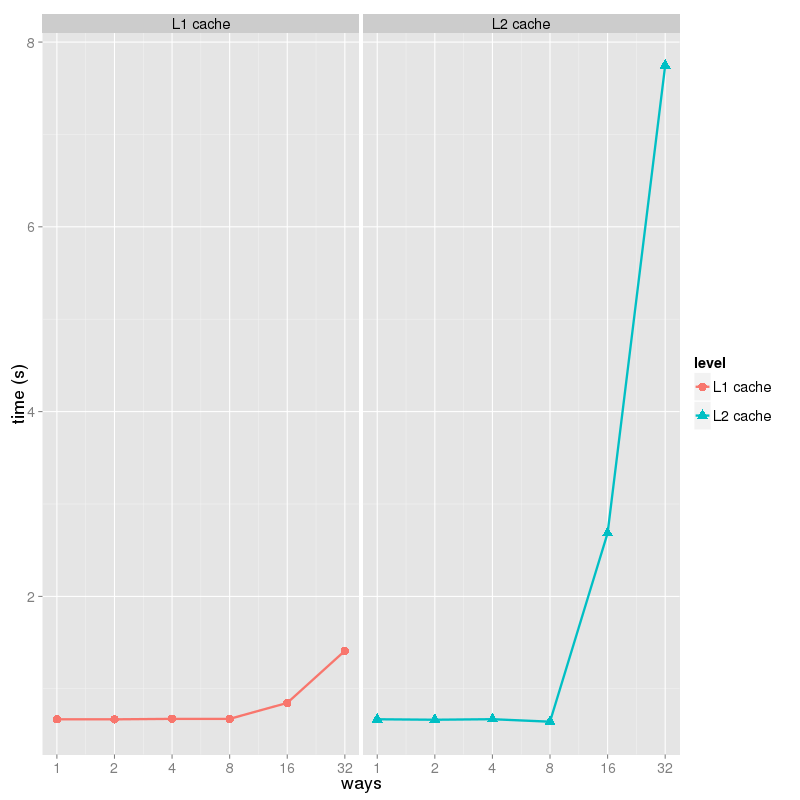
image

实验数据分析

枚举到16倍cache大小时，时间剧增，因此L1 data cache的相连度为上一次枚举的值：8。

枚举到16倍cache大小时，时间剧增，因此L2 data cache的相连度为上一次枚举的值：8。

Cache写回策略

策略

对于一倍和两倍cache大小的数组，顺序访问测量时间，若近似相等则为write-through，否则是write-back。

设计原理

write-through在写入时一定会访问内存，表现和all miss类似，所以可以比较两种模式的运行时间。

实验结果

% ./a -r $[32*1024]
hit             0.159024
miss            0.334086

% ./a -r $[256*1024]
hit             0.561438
miss            0.722406

实验数据分析

对于L1 L2 cache大小，两种模式时间都有较大差异，故都是write-back。

Cache替换策略

设计原理

当数组大小刚好大于cache大小并且以循环顺序模式访问时，标准的LRU表现会像是all miss。

这里的测试较为困难，因为两种测试在代码或数据上至少有一项不同，会有很多情况影响运行结果，很难设计反映LRU自身特性的测试。

实验结果

% ./a -s
all miss                3.497159
lru miss                3.312766

实验数据分析

数组大小刚好大于cache大小并且以循环顺序模式访问时，实际时间比all miss略少，猜测CPU使用的不是标准的LRU算法。实际上Ivy-Bridge使用的是一种变化的LRU。

矩阵乘法优化

原始代码分析

矩阵(b[][])以column-major order访问，导致cache频繁miss而性能低下。另外原来的代码在我的Linux系统里无法编译通过，因为缺少了cstring头文件，源代码的头文件部分添加了。

考虑这样一个tall ideal cache model： cache line大小为，cache总大小为，方阵的边长为。 Cache是full associative的，并且cache line的替换采用最优策略(系统实际采用的变形LRU策略是最优策略的一个近似)。另外有个tall-cache assumption，即假设cache line的数目大于cache line大小即，这样保证我们平行做常数个扫描时不会因为cache大小而需要改变策略。

当时，矩阵都能存储在cache中，每个矩阵都需要次内存传送，整个算法时间复杂度为，需要次内存传送。

当时，cache无法存储一个完整的矩阵。矩阵的每个元素的计算都需要列访问矩阵。Cache只有个cache line，当时，即使采用最优缓存替换策略，也会导致在循环中每次增加后之前读入的存储元素的所有cache line全部失效，每个元素的计算都需要次内存传送。整个算法总共需要次内存传送。

交换三层循环次序

通过把i,j,k的三层循环次序修改为i,k,j能使其中两个矩阵的都成为row-major order访问， 提高了效率。代码参见：src/matrix_mul.cpp。

对于的每一个元素的计算，最多需要次内存传送，整个算法需要次内存传送。

运行结果：

% ./matrix_mul
time spent for original method : 14909765 ms
time spent for new method : 803459 ms

k,i,j的循环次序也能提高效率，但效果略差于i,k,j，原因是d[i][j] += a[i][k] * b[k][j];中两个数组的第一维是i，一个是k，对于i,k,j的循环次序，两个数组更容易被缓存。

% ./matrix_mul
time spent for original method : 14682039 ms
time spent for new method : 1024053 ms

另外使用icpc -O3编译会发现原始版本也很快，改进效果很不明显：

% icpc -v
icpc version 14.0.2 (gcc version 4.8.0 compatibility)

% ./matrix_mul
time spent for original method : 842223 ms
time spent for new method : 817969 ms

查看icpc -O3 -opt-report的输出可以发现：

<matrix_mul.cpp;38:38;hlo_linear_trans;main;0>
LOOP INTERCHANGE in loops at line: 40 42 
Loopnest permutation ( 1 2 3 ) --> ( 1 3 2 )

编译器做了loop interchange优化，把循环次序修改为i,k,j。

测试了GCC的Graphite loop transformation infrastructure，但是-floop-interchange似乎没有起效。

转置b使得b变为column-major order访问

另外一种方式是在乘法前转置b使得它的访问变为row major顺序，乘法后再转置回来：src/matrix_mul_transpose.cpp。

当时，矩阵的每个元素的计算需要最多次内存传送，所有个元素需要次内存传送，优于原始的。

运行结果：

time spent for original method : 14655990 ms
time spent for new method : 3795749 ms

使用Intel VTune Amplifier XE进行性能剖析发现swap的总开销为0.01秒，k所在循环执行时间为3.780秒，而原来的方法的k循环执行时间为12.926秒。转置带来的代价很小。另外这里使用的转置方法不是考虑cache的情况下最佳的，使用loop tiling的方式会更好。

另外代码使用到了algorithm头文件的swap。

Cache-aware blocked matrix multiplication

这个方法应用了loop tiling的技巧，把原矩阵分割成若干个边长为的子矩阵，满足子矩阵能在cache里存储下，即。这样计算子矩阵的乘积只需要次内存传送，原矩阵有个子矩阵，总的内存传送次数为@Hong81。

源代码见src/matrix_mul_block.cpp。

% ./matrix_mul_block
time spent for original method : 14722019 ms
time spent for new method : 2165467 ms

代码中t += a[i][k] * b[k][j];是瓶颈，只涉及了两个矩阵，因此可以取为。

我在CPU为Intel(R) Xeon(R) CPU E3-1220 V2 @ 3.10GHz的服务器上测试不同块大小的运行时间：

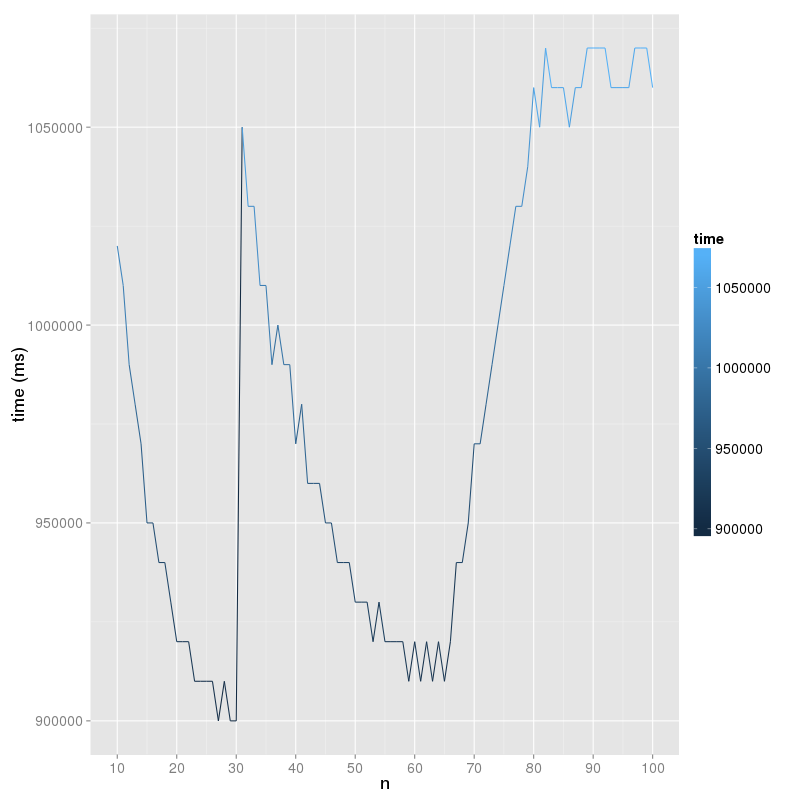
image

根据L1 cache大小(32KiB)计算出，可以发现左右运行时间确实较短。另外在左右的低谷不知道是什么原因。另外尽管不太明显，但当为的约数时比临近的取值要稍好一些。

扩展

对于其他更复杂的问题，cache-oblivious algorithm的写法可能会更好。

矩阵用row-major order以外的方式存储如von Emde Boas layout可能会更块。

分支预测

预测方法概述

Static prediction

不依赖代码执行历史进行预测，比如根据opcode预测总是跳转或不跳转。一个比较好的方法是displacement based，预测后向跳转总是发生，而前向跳转总是不发生。另外还可以根据分支的可能性使用不同的指令，编译器在生成代码时生成不同的opcode提示CPU。

Saturating counter

常用2个bit记录4个状态，实现为bimodal predictor，4个状态分别表示：

  • Strongly not taken

  • Weakly not taken

  • Weakly taken

  • Strongly taken

每当分支结果产生，就用saturating的加减法操作更新计数器。如果跳转则令计数器表示的可能性增大，即往下移动，不跳转则往上移动。

使用2个bit而不是1个bit的好处在于常见的循环结构，如果条件跳转在循环体后面，则后向跳转比较多，该指令的历史将是一串“跳转”后跟一个“不跳转”。计数器将很快表示strongly taken且即使碰到最后的“不跳转”， 也只是把状态变为weakly taken，下次执行循环时人能正确预测。如果条件跳转在循环体前面，则前向跳转比较多，该指令的历史将是一串“不跳转”后跟一个“跳转”，情况和后向跳转类似。

Local branch prediction

对每条条件分支指令维护历史状态，预测时根据当前指令的历史状态进行预测。这种方式对数据存储方式有较大要求，很容易占用过多存储空间。这个特征的实用性较小，我看到的很多较好的预测器都不使用这个特征。

Global branch prediction

所有条件分支指令共享一个保存历史的缓冲区，历史信息就是最近的若干次条件分支是否发生的bitset。

Path history based predictor

把最近执行的指令地址纳入考虑范围。如果取完整的地址会比较浪费，JWAC-2中André SSeznec的实现中取最近若干条指令地址的最低位的bitset作为特征，可以这么做的原因是x86-64指令长度不规整。

Multiple branch histories

最初的基于global history的方式只使用一个表对某一特定长度的历史进行预测，@mcfarling里描述了一个使用多个历史长度的预测器。

Neural branch prediction

有很多研究使用感知器搭建神经网络进行分支预测，优点是很容易利用长历史，但涉及到的串行运算较多(比如感知器涉及到两个向量的乘积)会导致较大的延时。

Branch target prediction

预测器介绍

gshare

实验框架中的默认预测器实现了@mcfarling中提到的gshare算法，从分类上说属于two-level adaptive predictor，可以在缓冲区条目中区分不同分支指令的历史，方法是把分支地址和global history异或后计算缓冲区的索引值。 索引得到的是saturating counter。比起直接用分支地址索引saturating counter，结合了global history后能更准确一些。

Idealized Piecewise Linear Branch Predictor

@daniel中描述的感知器，以当前条件分支前的各条分支指令和相隔距离，以及该分支自身的local history作为特征训练感知器。 当前指令，与它产生相互作用的global history中的另一条指令，和它们的间隔有三维，状态数很多， Daniel A. Jiménez的实现中分配了一个很大的数组储存感知器的向量，把这三维hash后计算得到数组中的下标。这里hash的下标没有考虑冲突的情况，可能是基于两个原因：

  • 避免引入额外的存储空间开销。感知器的向量系数可以用一个字节或几个比特表示，如果采用类似separate-chaining的方法，指针的引入将带来极大的开销。

  • 延迟相比准确性更重要。如果采用open addressing这样的方法，会增大延时，得不偿失。

实现中还会根据训练数据估测workload的类型，动态调整参数。另外一段时间后会清空训练的感知器的向量，我觉得原因可能是程序通常具有阶段性，不同阶段的表现出入较大，作者是希望放置上一阶段的训练结果影响到之后阶段的预测。但测试发现去除清空操作后效果更好。

Daniel A. Jiménez的预测器简单修改适配实验框架后测试所有traces得到的平均MISPRED_PER_1K_INST值为3.6。

TAGE

第二次实验中我实现了@tage中描述的TAGE算法，这是一种PPM类型的预测器@ppm，由一个基础分支预测器(采用saturating bimodal predictor)和若干个长度不同的PPM(prediction by partial matching)预测器组成。

每个PPM预测器有一个内置的长度，它是一个two-level adaptive predictor，每个记录项就是(分支指令发生前history中最近项,分支指令地址)二元组到一个saturating counter的映射，这个saturating counter就像bimodal predictor那样记录实际的跳转情况。

预测阶段

预测时，找到内置长度最大的找得到匹配项的PPM预测器，令其saturating counter指示的结果为。再找到内置长度第二大的找得到匹配项的PPM预测器，令其saturating counter指示的结果为， 如果找不到则采用bimodal predictor的结果作为。

如果和相同则采用作为最后预测结果。否则如果对应的saturating counter取值为弱结果且之前历史上有多次和取值不同而预测正确的情况，那么就会采用作为最终预测结果。

PPM检索方式

PPM预测器的每个记录项是(分支指令发生前history中最近项,分支指令地址)二元组到一个saturating counter的映射。如果要完整记录标识的分支指令发生前history中最近项，需要位存储空间。不同的项有个，还要乘以地址空间，空间无法承受。

实现中每个PPM预测器根据其内置长度分配一定的容量，每一项用一个位的hash值来表示(分支指令发生前history中最近项,分支指令地址)。

Global history只记录最近的若干条记录。 设global history中第个条件分支指令的发生情况为，为1代表条件分支跳转了，0代表未跳转。

令槽位的索引值为，的取值为。令当前时刻为，二进制的第位即gi>>i & 1的值定义为。 实现为一个circular shift register，可以根据上一时刻的值计算当前时刻的值：$(g {cir}1) a_t (a{t-l} (l c)) $。

根据探测PPM预测器的相应槽位，为了减少hash值相同引起的错误，每一项还使用另一个散列值来验证。

更新阶段

用当前条件跳转指令是否发生跳转来更新global history， 并把(global history中最近项,分支指令地址)表示的项添加到所有PPM预测器中。

如果之前的最终预测结果(有两种可能取值，和)错误且也错误(因为saturating counter为弱取值导致被取代)就可能需要在预测表中添加新项，但要保证并不是最长的。这样下次碰到同样的模式时，还会匹配上，但我们新添加的项更长，就能覆盖当前的匹配结果。

PPM根据地址和最近若干项global history计算得到的tag(hash值)很可能会冲突。冲突时保留原来的项还是取新的项？为此，每个条目还要记录一个 bit。

bit

每个PPM预测器条目还要保存一个 bit，表示该条目是否有用。

对于一个条目，如果之前有很多次预测以它为且它预测正确了而预测失败，则该条目是有用的。

如果以它为且它预测正确时也都正确，那么这个条目用处不大，因为如果没有它，将成为最长匹配项且也能预测正确。它的槽位应该留给和它hash值相同的其他条目。

当添加新项发生冲突时会考察已有项的 bit，如果为0则替换，否则在内置长度更大的PPM预测器中添加。

如前文所说，当预测正确而预测失败时要更新的条目的。这里的像某种cache，需要设计一个置换策略，可以采用时钟算法，定期清空。

由于有 bit的存在，添加新条目时可以一次性添加若干项，使得记录项更不易失。实现中我最多添加4项。但要注意添加的项不能在相邻的PPM预测器中，否则较长的项的无法变为1，会很容易被替换掉。

存储需求

我的实现运行时会在stderr输出空间占用：

storage: 260348 bits = 32544 bytes

其中包含了一些标量变量的空间占用。

占空间的主要是每个PPM预测器储存的项，各个PPM预测器容量不尽相同，为512项到2048项。

结果

LONG-SPEC2K6-00                1.531
LONG-SPEC2K6-01                7.510
LONG-SPEC2K6-02                0.364
LONG-SPEC2K6-03                0.575
LONG-SPEC2K6-04                8.590
LONG-SPEC2K6-05                4.911
LONG-SPEC2K6-06                0.635
LONG-SPEC2K6-07                9.259
LONG-SPEC2K6-08                0.670
LONG-SPEC2K6-09                3.628
LONG-SPEC2K6-10                0.670
LONG-SPEC2K6-11                0.670
LONG-SPEC2K6-12               11.498
LONG-SPEC2K6-13                6.131
LONG-SPEC2K6-14                0.001
LONG-SPEC2K6-15                0.332
LONG-SPEC2K6-16                3.278
LONG-SPEC2K6-17                2.487
LONG-SPEC2K6-18                0.057
LONG-SPEC2K6-19                1.082
SHORT-FP-1                     1.226
SHORT-FP-2                     0.518
SHORT-FP-3                     0.018
SHORT-FP-4                     0.094
SHORT-FP-5                     0.029
SHORT-INT-1                    0.146
SHORT-INT-2                    4.927
SHORT-INT-3                    8.000
SHORT-INT-4                    0.563
SHORT-INT-5                    0.301
SHORT-MM-1                     7.282
SHORT-MM-2                     9.359
SHORT-MM-3                     0.070
SHORT-MM-4                     1.161
SHORT-MM-5                     4.413
SHORT-SERV-1                   0.901
SHORT-SERV-2                   0.872
SHORT-SERV-3                   3.228
SHORT-SERV-4                   2.301
SHORT-SERV-5                   1.842

AMEAN                          2.778

而baseline程序的结果如下：

LONG-SPEC2K6-00                3.974                                                                                                                  [2/1974]
LONG-SPEC2K6-01                8.406
LONG-SPEC2K6-02                5.176
LONG-SPEC2K6-03                5.658
LONG-SPEC2K6-04               10.739
LONG-SPEC2K6-05                5.780
LONG-SPEC2K6-06                4.160
LONG-SPEC2K6-07               14.062
LONG-SPEC2K6-08                1.911
LONG-SPEC2K6-09                5.502
LONG-SPEC2K6-10                3.710
LONG-SPEC2K6-11                3.929
LONG-SPEC2K6-12               12.844
LONG-SPEC2K6-13                9.880
LONG-SPEC2K6-14                4.687
LONG-SPEC2K6-15                2.648
LONG-SPEC2K6-16                4.435
LONG-SPEC2K6-17                5.464
LONG-SPEC2K6-18                1.525
LONG-SPEC2K6-19                2.599
SHORT-FP-1                     3.479
SHORT-FP-2                     1.061
SHORT-FP-3                     0.443
SHORT-FP-4                     0.258
SHORT-FP-5                     0.788
SHORT-INT-1                    7.347
SHORT-INT-2                    7.669
SHORT-INT-3                   11.784
SHORT-INT-4                    2.250
SHORT-INT-5                    0.438
SHORT-MM-1                     9.172
SHORT-MM-2                    10.601
SHORT-MM-3                     4.267
SHORT-MM-4                     1.811
SHORT-MM-5                     5.651
SHORT-SERV-1                   3.646
SHORT-SERV-2                   3.665
SHORT-SERV-3                   5.870
SHORT-SERV-4                   5.324
SHORT-SERV-5                   5.208

AMEAN                          5.196