2023-01-13

人工智能导论

文本分类

算法描述

Naive Bayes classifier

采用multinomial Naive Bayes model，文档中单词分布视为multinomial的，单词之间相互没有影响，文档被归入某一分类的可能性视为其中所有单词出现在分类中的概率的乘积，即：

实现中根据最大后验概率把文档归入分类，即：

取对数后得到：

实现中为每个候选分类设置一个分数值，初始化为该分类的先验概率，之后对于查询文档中的每个词，用更新这些分数值。最后选择具有最大分数值的分类作为分类结果。

Support vector machine classifier

特征选取：

预料中单词总数约为15000，根据公式计算每个文档中各个单词（特征）的权值。实现中把换成了，后者的准确率更为理想。

运行结果

准确率

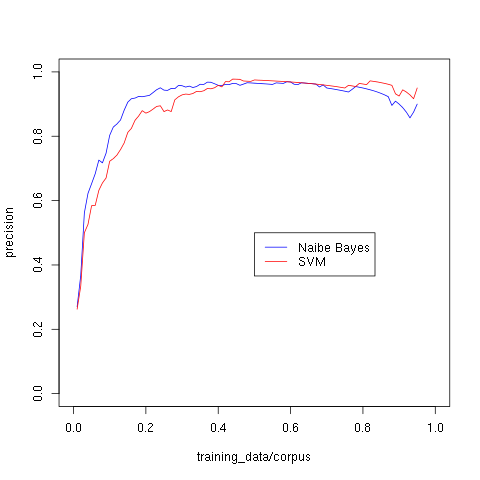
把测试数据划分成训练数据和测试数据，以训练数据占语料的比例为横轴，测试数据准确率为纵轴绘得下图：

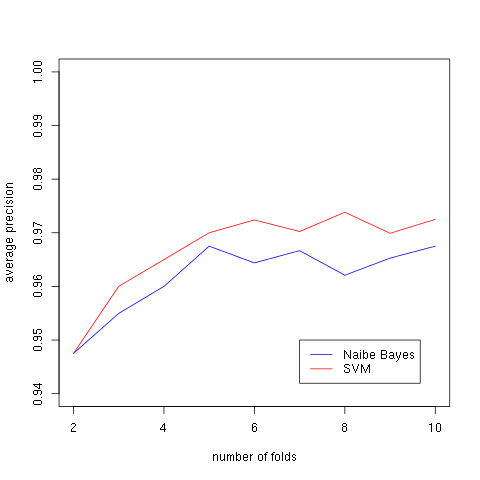
交叉验证

实现

为C++ 11实现，另有的OCaml实现。

执行即可编译C++ 11实现，生成。

在程序执行的工作目录创建文件表示训练数据，其格式如下：

# hardware
/tmp/data/c4_comp.sys.mac.hardware/52446
/tmp/data/c4_comp.sys.mac.hardware/52439
/tmp/data/c4_comp.sys.mac.hardware/52342
# atheism
/tmp/data/c1_atheism/54258
/tmp/data/c1_atheism/54249
/tmp/data/c1_atheism/54163

其中和代表分类名，之后的文件名则为具体的训练数据文件名。

再创建表示测试数据，比如：

# hardware
/tmp/data/c4_comp.sys.mac.hardware/52193
/tmp/data/c4_comp.sys.mac.hardware/52090
# atheism
/tmp/data/c1_atheism/51060
/tmp/data/c1_atheism/51119

格式和相同。

运行即返回Naive Bayes分类的准确度。

运行即返回Naive Bayes分类的准确度，同时输出每个测试数据的分类结果。

运行即返回SVM分类的准确度。

运行即返回SVM分类的准确度，同时输出每个测试数据的分类结果。

四子棋

课程设计是实现四子棋AI。

算法描述

本次程序实验中我使用了Monte Carlo Tree Search算法，这类算法把博弈树搜索和随机算法结合了起来， domain-specific knowledge是可选的，这意味着无需像minimax那样实现一个对未结束局面估价的函数。

在每一回合收到getPoint指令后，程序建立一个根节点表示当前局面。每个节点连向孩子的边代表处于该节点表示的局面下可以选择的着法，而相应的孩子就是选择该着法后转移到的局面。树一开始只包含根节点，在之后的expansion过程中节点会被添加到树中。

然后执行若干次迭代过程，每次迭代都会依次执行selection、expansion、simulation和backpropagation四个过程。

Selection。从根出发，根据tree policy走到一个孩子节点，重复此过程直到碰到一个可扩展的节点为止。可扩展的节点指的是带有未访问孩子的节点。
Expansion。此时我们已经走到了一个可扩展节点。根据tree policy选择未探索过的着法中最有探索价值的，给当前节点添加一个孩子并走到这个孩子节点。
Simulation。根据default policy在当前节点表示棋盘下模拟双方对弈。
Backpropagation。根据对弈的结果更新当前节点及其所有祖先的统计信息。

MCTS是这一类算法的统称，通过选取适当的tree policy和default policy就得到了一系列具体算法。对于tree policy，我使用了Upper Confidence Bounds for Trees(UCT)算法，根据公式：

来选择具有最大值的孩子节点。其中，是根据统计信息计算出来的表示对应着法是否优秀的量。为当前节点的访问数，为孩子节点的访问数，为一个大于0的常数。

公式中第一个加数表示孩子节点的优秀程度(exploitation)，第二个加数表示探索度(exploration)。

Exploitation高代表选择该孩子节点对应的着法，模拟对弈的结果中有利局面多，所以该孩子节点对应的着法较为优秀。
Exploration高代表选择该孩子节点对应的着法的尝试次数不够多(因为在分母中)，需要进一步探索。

优化

位棋盘

需要处理的最大棋盘规模为，可以用一个uint64_t表示三列，那么12列就只需要3个uint64_t来表示，可以看作一个uint192_t，其各个二进制位对应的棋盘上位置如下：

 64-bit         64-bit        64-bit

0f 1f 2f 3f | 4f 5f 6f 7f | 8f 9f af bf
.. .. .. .. | .. .. .. .. | 8. 9. .. ..
01 11 21 31 | 41 51 61 71 | 81 91 a1 b1
00 10 20 30 | 40 50 60 70 | 80 90 a0 b0

对于胜负的判定，只需要用移位操作和与运算即可在在时间内求出。比如要判断白棋在竖直方向上是否连成四子，只需要取出其位棋盘，判断w & w>>1 & w>>2 & w>>3，类似地可以判断水平方向、斜线方向上是否连成四子。

另外，不储存每一列的数组也可以在时间内求出所有可以候选着法。方法是对于每一列，计算二进制表示里从下到上连续的1的个数，这个通过加1后计算最低位的1实现。

快速log

改用https://github.com/herumi/fmath的实现后搜索性能有明显提升。

省略父节点

父节点指针仅用于backpropagation过程，而这一过程中访问到的祖先节点都在之前select步骤时访问过了，所以可以用栈保存根节点到当前节点路径上的所有节点，无需存储父节点指针，节省了空间。

候选着法优化

Playout过程中可以只生成一次所有着法，之后每步只需时间。

旋转根

第一次收到getPoint指令前程序需要完整地构建树，但之后收到getPoint后可以根据双方选择的着法把根变换到原来根节点的某个孙子节点，这样可以继承之前回合搜索的结果。

动态分配内存开销会比较大，我实现了一个内存池，用双链表储存尚未分配的节点。节点的两个信息score及visited刚好可以用作双链表的两个指针，节省空间。

实现该方法后需要实现子树的析构操作，比较耗时。测试发现这样做得不偿失，因此没有采用。

MCTS Solver

实验效果不理想，原因可能是selection和backpropation过程中更新game-theoreticvalue的代价太大了，导致迭代次数大幅下降。

并行

主要有两类并行模式：Leaf parallelisation和root parallelisation，前者是并行执行多个playout操作，后者是并行计算多棵搜索树。实现中采用了前者，用OpenMP实现了简单的并行模式。

对局结束后需要释放树占用的资源，程序中实现一个singleton对象，该对象的析构函数会释放树占用的资源。

如果允许使用多线程，请在Visual Studio配置属性的C/C++选项卡的语言选项里添加“OpenMP支持“，并修改MCTS.cc开头的#define NTHREAD 1，修改为#define NTHREAD 3，或系统可用线程数。